Disclaimer (added after many comments on Twitter and via email): I am presenting a very SH0ES-centric view of the problem, as is George’s paper. Of course I believe the H0 tension is really about H0 (or the sound horizon), but only when you enlarge your view to late-time probes beyond SH0ES. My post with its new title should be seen as purposely being a SH0ES-centric view of the issue. I’ve fixed a few points to make this clearer.
INTRO and context (SKIP TO the “physics starts here” section below if you want to cut to the chase)
Initially this week’s blog post was meant to be a standard one - the usual 2-3-paragraph reviews of 3 interesting preprints. And, for the record, the preprints I would have reviewed this week are (in this order) George Efstathiou’s “To H0 or not to H0” 2103.08723, Rittick Roy et al.’s 2103.08978, and Jack Burns et al.’s 2103.08623 which isn’t really a preprint in a strict sense, but rather a response to DOE request for information on a potential lunar farside radio telescope - but a detailed one for the matter. But, as I’ve already tried a few different things on my blog this year, I thought I’d try something slightly different this week too. In particular, I’ll try to provide a much more in-depth coverage of George’s paper, for several reasons I’ll discuss shortly. This will be intertwined with personal considerations on what the Hubble tension really is and how we really should start to think about and approach the problem moving forward.
So, why cover this paper in particular? There are at least 5 reasons:
despite there not being anything terribly new in this paper as I myself told George, I still think it’s among the single most important papers written on the H0 tension (a name which in itself is a misnomer, as I will argue later), and I believe the important message of this paper stands out more clearly compared to earlier papers which made similar arguments.
many people have independently asked me what my thoughts on the paper are (probably because George put my name in the acknowledgements?). I can’t answer all the emails/whatsapp messages else I’d be doing nothing else all day, so I hope this post will do.
there’s been much discussion about this paper on Twitter and other social media. From a quick glance, it seems to me like many have misinterpreted the main message of the paper. So I hope this post, if you take the time to read it, will help clarify this.
this paper touches on a mistake, frequently repeated in the literature, which I’m rather sensitive about (misuse of local H0 prior). So I want to take the time to explain it clearly.
I am a fan of Hamletian titles (see my own arXiv:1807.04672).
The physics starts in a second. Before that, a disclaimer: this is a blog post, not a scientific paper. In some parts I will be intentionally provocative, with the aim of getting the message across more clearly. Feel free to disagree with what I write, and if so shoot me a comment below or an email. I should also note that similar points have been made earlier in two papers I actually already happened to cover in this blog: these are Benevento et al.’s PRD 101 (2020) 103517 [arXiv:2002.11707], or B20 hereafter (which I covered in my 2020 Week 9 post), and Camarena and Marra’s arXiv:2101.08641, or CM21 hereafter (which I covered in my 2021 Week 3 post). See also my disclaimer at the top of the post, about this presenting a very SH0ES-centric view of the problem. Please keep this in mind when reading my post.
PHYSICS STARTS HERE
The H0 tension has nothing to do with H0 (from a SH0ES-centric perspective). There, I’ve said it, and no I haven’t lost my mind due to the pandemic. OK maybe I should have said “Focusing only on H0 obscures the real story”. So now you’re thinking: “Sure, because the H0 tension should really be phrased as a sound horizon tension”. Well, that’s true, but from a SH0ES-centric perspective, the real heart of the H0 tension has nothing to do with the sound horizon r_s. It has to do with the SNeIa absolute peak magnitude M_B, because the SH0ES team doesn’t actually measure H0. Or rather, they don’t directly infer H0 (where “directly” is the keyword).
Let me put it differently. There are three different layers of interpretation of what the H0 tension really is, from the point of view of SH0ES. In order of increasing correctness, the H0 tension is:
1a. the mismatch between the SH0ES value of H0 and the value inferred from CMB temperature* data from Planck assuming LCDM
1b. *temperature and polarization data
2. the ~10 Mpc mismatch between the value of the sound horizon r_s inferred if I anchor BAO measurements to the SH0ES value of H0, versus the LCDM value of r_s (with prior on omegabh2 from the CMB and/or BBN)
3. the 0.2 mag mismatch between the value of M_B needed to fit Pantheon Hubble flow SNeIa if they are calibrated through the Cepheid distance ladder versus if they are anchored to the inverse distance ladder by combining them with BAO data and a LCDM prior on the sound horizon
It is the subtle difference between 2. and 3. which George’s paper is partly about. In broad brush, point 1a. stresses the importance of CMB temperature data, 1b. of CMB polarization data, and 2. of BAO data. Point 3. stresses both the importance of Pantheon Hubble flow SNeIa and the danger associated to a misuse of the SH0ES H0 prior. Simplifying a bit, if one wants to solve the H0 tension, one should get a high H0 from CMB (temperature+polarization)+BAO+Pantheon without the aid of a SH0ES H0 prior. Nothing new so far. Below is a visual representation of this 0.2 mag offset, taken from the bottom panel of Fig. 3 of CM21.
Credits: Camarena & Marra, arXiv:2101.08641
Let me now elaborate on what I wrote earlier about the SH0ES team not actually measuring H0. This is nicely explained in George’s paper on Page 2. How do distance ladder measurements work? In the first rung, one uses local geometric distance anchors to reach astrophysical objects containing Cepheids, to calibrate the Cepheid period-luminosity relation. This relation is then used to move further towards host galaxies containing both Cepheids and SNeIa, and produce a constraint on M_B. Finally, with the inferred value of M_B, one uses the magnitude-redshift (or equivalently, luminosity distance-redshift) relation of Pantheon SNeIa in the redshift range 0.023<z<0.15 to convert this value of M_B into a value of H0. Essentially, from the inferred value of M_B, the SH0ES team “works backwards” to find the incercept of the Pantheon SNeIa magnitude-redshift relation, fitting a low-z cosmographic expansion to the luminosity distance as a function of redshift.
Can you already see where the “problem” is? 0.023<z<0.15. The lower range of this interval is not 0. In other words, the SH0ES team is not directly measuring H0 in the sense of H(z) in the limit z->0, but rather is extrapolating the value of H0 one gets from the z>0.023 Hubble diagram, given the measured value of M_B. Imagine, however, that something funny happened at z<0.023. Say, for instance, that the expansion rate suddenly increased drastically so that H0 increased equally dramatically. The SH0ES team would still infer the “low” H0 indicated by the z>0.023 portion of the Hubble diagram. As George puts it, they would be “oblivious” to any sort of late-time transition (which could be a sudden phantom transition, a sudden conversion of dark matter into dark energy, or something even more drastic). So if such a late-time transition happened, SH0ES would actually be measuring, or rather inferring, the “wrong” value of H0.
It is thus of paramount importance to make a distinction between the “true” and “SH0ES-like” values of H0. This is nicely exemplified in George’s Eqs.(10a) and (10b), which I copy below (note that similar distinctions were also made in B20 and CM21).
Credits: Efstathiou, arXiv:2103.08723
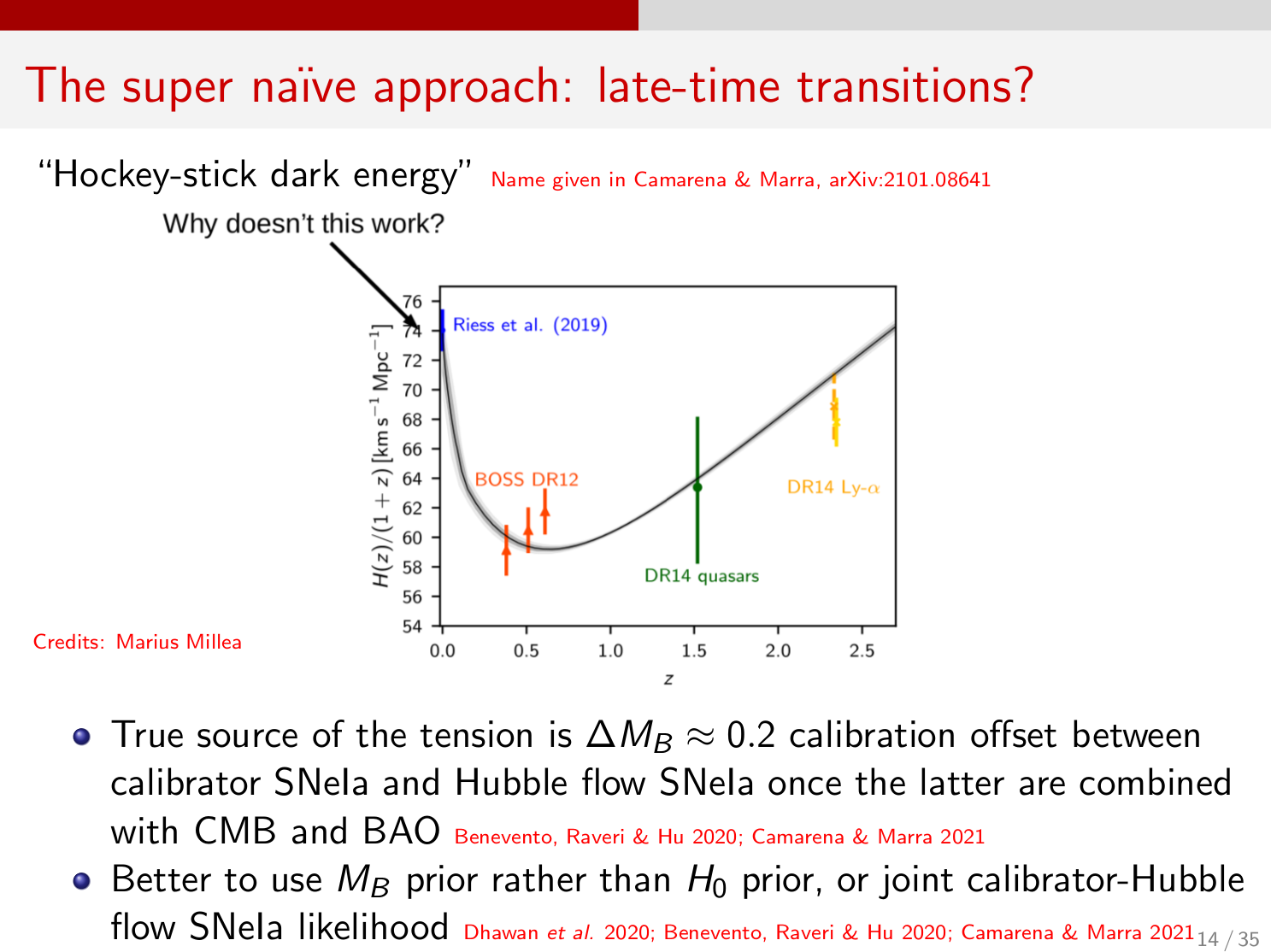
So let’s take a step back and think about how we interpret the Hubble tension. If we interpret the tension as pertaining to the SH0ES value of H0, we should not compare the “true” H0 we infer from CMB+BAO+Pantheon+whatever else to the SH0ES H0, but rather compare the latter to the “SH0ES-like” H0 we infer from CMB+BAO+Pantheon+whatever else. For most models, this makes no difference, but for models which predict something crazy going on at late times, it does. Let me stress this again: you have to deliberately compare what might actually be the “wrong” H0 if you want to compare your H0 value to SH0ES. If you manage to get a high H0 doing something crazy at super-late times, it doesn’t matter because SH0ES would not be sensitive to this and would still infer a low H0, so you’re back to where you started. And of course, if you do this at less late times, say at z>0.15, then you run into trouble with the high-z Pantheon magnitude-redshift diagram, so you’re again back to where you started. In other words, something like what is shown below won’t work, even if you make the transition occur at z<0.02, or rather especially because of that!
Credits: Marius Millea
(Aside: if you want to solve the problem at late times, then you need to find something which fixes the SNeIa absolute magnitudes, e.g. transitions in Newton’s effective constant at low redshifts as considered by Alestas, Kazantzidis, Marra, and Perivolaropoulos in 2012.13932 and 2102.06012, or by Desmond, Jain, and Sakstein in 1907.03778 and 2003.12876, or by Cai et al. in 2102.02020. Some of these scenarios are contrived to say the least, but as a proof of principle they might work.)
But now you’re saying: certainly all this sounds a bit complicated. Well it does, but for the reason that we’ve been thinking about the H0 tension in the wrong way. If you think about the H0 tension from the SH0ES perspective as being a M_B tension, all these complications magically disappear. This shows (shoes?) the important distinction between raising the “true” H0 to the SH0ES value and truly solving the H0 tension, i.e. the 0.2 mag calibration issue with the part of the Hubble diagram where the tension is inferred. If I now circle all the way back to the first thing I wrote, i.e. that the H0 tension has nothing to do with H0, at least from a SH0ES-centric point of view, I sincerely hope what I wrote earlier now sounds less crazy.
From the SH0ES perspective, the term “H0 tension” is a very serious misnomer. If discussing the CMB vs SH0ES discrepancy, I strongly encourage anyone, whether senior researchers, students, and especially popular science journalists, to refrain from using the term “H0 tension” anymore. A good name would be “Supernovae absolute magnitude tension”. If this sounds too long, “SH0ES tension” will do just fine, as it reflects the fact that the tension can be rephrased as having to do with the value of H0 one would infer from a SH0ES-like analysis, which is oblivious to anything happening at too late times. Of course, this is a very SH0ES-centric view of the problem. Once you enlarge the late-time view to include other probes (which you should!!!) which also find H0 in the low 70s (TRGB, H0LiCOW, water megamasers, BTF relation, SBF, etc.), the reality that this really is an “H0 tension” emerges. But let me stress once more that from a very SH0ES-centric point of view, the problem is with m_B.
This brings me to the next important point, pertaining to misuse of the local H0 prior. Anyone who has been reading this blog for long enough knows that I’ve been complaining about this since forever, although for a slightly different reason. The reason why I complained is that every day I see many analyses which just include a local H0 prior without investigating whether such an inclusion is actually warranted. To read my complaints in more detail, just head to my 2020 Week 26 post. In other words, say I take CMB+BAO+Pantheon. If I don’t get a high enough H0 from this dataset combination, I am not allowed to include a local H0 prior, simply because I would be adding data in tension with the rest of my other data. The result would be to artificially increase H0 and bring me to claim a better “solution” (?) to the tension than what I really have. Not to mention that this carries an aftertaste of double-counting data. Anyone with a basic smattering of statistics will easily get why this is a problem, yet this is a mistake which appears extremely frequently in the literature (9 papers out of 10 or more?). A nice paper discussing this issue well in the context of a specific model, carefully dissecting whether or not the use of the H0 prior was legitimate or not, is Brickmann et al'.’s 2012.11830 (although it too falls into the trap I discuss in the paragraph below).
But the misuse I am talking about now, and which George also discusses in his paper (see the second paragraph of the Conclusions) is more serious. The point is that it doesn’t make sense to include a prior on H0 in first place, even in the improbable event that you managed to get a high H0 from CMB+BAO+Pantheon. The reason is that you aren’t necessarily comparing apples to apples, as you are treating information pertaining to the “SH0ES-like” H0 as if it were pertaining to the “true” H0. Also, by doing so, you are obscuring the real source of the tension.
So how to proceed? Well, first of all, don’t include any SH0ES information: why would you want to double-count data or play dirty on the way towards solving the tension? But if you still wanted to proceed, then the correct way of including the SH0ES information is through a prior on M_B. How to do this in practice? You basically have to convert the SH0ES H0-like quantity (and uncertainty) to an equivalent M_B (and uncertainty), which you can do e.g. following Eqs.(10) and (11) from Benevento et al.’s paper, see what I copy below.
Credits: Benevento, Raveri & Hu, PRD 101 (2020) 103517 [arXiv:2002.11707]
Or you can use the code CM21 kindly made publicly available on GitHub (their patch to MontePython to implement the M_B prior is now available here). And, finally, don’t forget that the step M_B -> H0 involves a cosmographic analysis, which may fail (for reasons I will discuss shortly below). On the other hand, M_B is an astrophysical measurement which is immune to cosmographic issues (although it is sensitive to other systematics, but of astrophysical rather than cosmological origin - which doesn’t mean these aren’t more serious). So, if you really (and do you really?!?!?) need to include the SH0ES information in your paper where you try to solve the SH0ES, please do it through a prior on M_B, or better still, don’t do it at all.
This is an extremely important point, and I somewhat wish George had expanded on it more than just a paragraph in the Conclusions. I am aware that many cosmologists are unaware of this subtlety, which is essentially the difference between points 2. and 3. in the different interpretations of the tension I presented above. But the same point is also made in B20 and CM21, so there really is no point ignoring this anymore. It is true that for many models this will not make a difference, but it is still important to keep in mind what is the cleanest way of transmitting the constraint from SH0ES (Adam Riess partially disagrees with the latter, see the “Note added” below for his point of view).
George’s paper makes another important point. Many of those who stop at point 2. in my interpretations of the tension think of it as being a tension between CMB+BAO vs SH0ES. Pantheon SNeIa aren’t always brought into the game. When they are, it is argued that the reason they are important is that they constrain the slope of H(z) at late times, which is important since BAO are only a handful of points, and you want to prevent models from doing something crazy in between the few BAO points. This is what Pantheon can do for you. However, there is another more fundamental reason why Pantheon data should always be included. And it is simply the fact that if you think back to what the tension really is, i.e. an M_B tension, then you see that “finding a solution that brings M_B into agreement with the SH0ES measurement […] necessarily involves analysing the Pantheon SNe sample” (verbatim from George’s paper). So, not only is there no good reason to leave out the Pantheon data, but it is simply wrong to do so if one wants to talk about the tension in first place. This much should be clear.
A few people on Twitter pointed out that “To H0 or not to H0” indicates that there is no room for late-time physics to solve the tension, whereas other works seem to say the same for early-time physics: see Jedamzik, Pogosian, and Zhao’s arXiv:2010.04158 and Lin, Chen, and Mack’s arXiv:2102.05701. I think there is no tension between these three papers, because an important adjective (adverb?) is missing: late-time physics alone can’t solve the tension, and neither can early-time physics alone. I personally believe that the tension, if there is indeed a tension, will ultimately require a combination of early- and late-time new physics to be solved.
A couple of weeks ago I gave a rather provocative talk at “A (Hubble) Tension Headache” (which you can watch on YouTube at this link) where I gave my view on the tension. I did mention this issue about M_B vs H0 but really just relegated it to one slide, shown below - in hindsight, I should perhaps have given it more visibility, which I’ll keep in mind for future talks.
Credits: yours sincerely
I closed my talk with 10 commandments which in my opinion any Hubble Hunter (or really SH0ES Hunter?) aiming to solve the tension should respect, as shown in the slide below:
Credits: yours sincerely
Somebody pointed out to me that the fourth commandment is a bit harsh and not really fair. So for my next talks (starting on Monday in Tel Aviv - see slides) I’m going to modify it to the following:
Credits: yours sincerely
(Aside: I hope my blasphemous editing of Moses doesn’t offend anyone religious (if so, please let me know). On this token, since many people have asked me in recent times, I am not religious in the strict sense, but I do believe in a Supreme Being (with a rather strong mathematical connotation to it) - it just does not happen to be any of the “usual” (e.g. Christian) ones.)
So, what is the take-away message? One is that a claimed solution to the tension should at the very least be tested against CMB temperature and polarization, BAO, and Pantheon SNeIa data. If SH0ES information has to be included, it should be included as a M_B prior, not a H0 one (or see the “Note added” below for Adam Riess’ thoughts on the matter). But I would personally discourage this in first place as I’ve said over and over. And of course, on the same token, if you want to include a TRGB M_B prior, you should use the Carnegie Supernova Project SNeIa rather than the Pantheon sample, for an obvious matter of consistency (see George’s footnote 9).
Since I’m on the topic, there are many other things I would like to discuss. One thing people often ask me is: are BAO and Pantheon data infallible? As for BAO data, if you want them to fail, you would need to invalidate some of the assumptions which go into the data reduction process, particularly pertaining to the assumption of a fiducial model. In particular, you would need to break the assumptions which make the Alcock-Paczynski scaling valid. In practice, to do this, you need strong deviations from an FLRW metric at late times, such as inhomogeneous cosmologies, large metric gradients, and so on. Asta Heinesen, a postdoc at ENS Lyon, is an expert on these topics, and I strongly encourage anyone interested in this to carefully read her papers, including but not limited to: 1908.11508, 2010.06534, and 2011.10048 (but check out her other papers too). These are highly technical and difficult to digest papers, but if you are interested I highly recommend you take the time to go through them. Interestingly, one of her later papers points out possible pitfalls of traditional cosmographic expansions, which might or might not be relevant for the Pantheon and SH0ES analyses. If you have any thoughts on this, please let me know. Of course, if the cosmological principle is invalid, Subir Sarkar would quite correctly point out that the concept of H0 is ill-defined in first place, as there is no one single number capturing the expansion rate of the Universe. The issue is, of course, whether the Universe is really that complicated a place on large scales. This is a fascinating topic, but one which I prefer to keep for a later discussion.
Finally, let me briefly mention one related point George often correctly brings up, at least since his lockdown paper (although not in his Hamletian paper). The TRGB measurement of H0 is often represented as being intermediate between Planck and SH0ES, but somewhat consistent with the two. In reality, one should not forget that the SNeIa samples used by the two teams are different. If the same SNeIa were used, this would reveal a 6σ calibration difference between TRGB and SH0ES. This is quite clearly shown in Fig. 5.1 of the lockdown paper. Resolving this controversy should be an important priority going forward. As are techniques for measuring H0 which do away with any distance ladder, such as strong lensing time delays, GW standard sirens, and distant masers. I can’t stress how important, in my opinion, this would be.
conclusions
This is the longest post I ever wrote on this blog, but for a good reason. First of all, I’ve always been sensitive to misuses of the H0 prior. Next, I think it’s important to phrase the tension in a way which is not misleading, and I think that from a very SH0ES-centric perspective, focusing on H0 and the “H0 tension” has been extremely misleading in this sense. Of course, once you enlarge the late-time view to include other probes (as you should do!), the reality that this really is an “H0 tension” emerges. But let me stress once more that from a very SH0ES-centric point of view, the problem is with m_B. Again, as a blogger I very much appreciate comments and feedback from my readers, so if you have any, please drop a comment below or in an email. And finally, if you think
this post was important, well written etc., I would appreciate if you could share/retweet/whatnot it.
Note added: Adam Riess was kind enough to give me some feedback on my post. One interesting point he made concerns what, in his opinion, is the proper way of transmitting the SH0ES constraint. Overall, Adam agrees with myself and George that people are making a big mistake in by taking the SH0ES H0 and Pantheon without recognizing their mutual dependencies.
Adam points out that the cleanest way of thinking about this is that SH0ES calibrates Pantheon, which itself uses a proxy value of H0=70. The SH0ES calibration of Pantheon is 5*log (H0/70.0) so for R21 (H0~73.2) this means 5*log (73.2/70.0) decrease in all distance moduli by ~0.097 mag plus a covariant error for all SN distances in Pantheon of the SH0ES H0 error of 1.8% minus in quadrature the tiny piece from Pantheon SNe which sets the Hubble flow for SH0ES (which is 0.5%) so net 1.7% of 0.037 mag in quadrature.
Adam’s recipe is then the following:
1. take Pantheon distance moduli and subtract 0.097 mag
2. assume a fully correlated error of every SN in Pantheon of 0.037 mag
Then take the Pantheon sample, and ignore any H0 prior. Or use the joint SH0ES-Pantheon likelihood developed in 2001.09260 and to be released shortly? Note that Dan Scolnic has also presented essentially this recipe on Twitter.
Thanks Adam for the feedback!


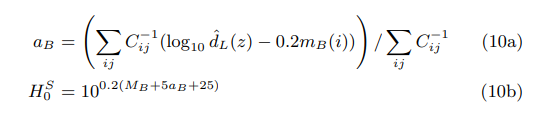

![Credits: Benevento, Raveri & Hu, PRD 101 (2020) 103517 [arXiv:2002.11707]](https://images.squarespace-cdn.com/content/v1/585d79ccf5e23158e7988f4b/1616153826547-IRTJZVFJB0JSAZDH1HDB/b20.png)